Student Question
“I don’t understand the difference between Covariance and Correlation. The book implies that Covariance and Correlation are the same things.” – Syed.
1-on-1 CMA Coaching Support
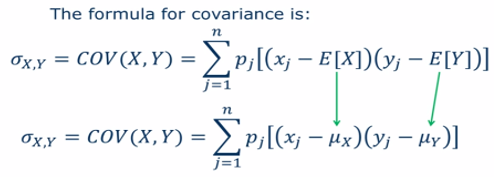
Here’s how to compute the covariance coefficient:
| Return | |||||
| Year | X | Y | (Xj – X̄) | (Yj – Ȳ) | Covariance Term |
| 2011 | -50% | -35% | -60% | -39% | 0.23 |
| 2012 | 33% | 33% | 23% | 29% | 0.07 |
| 2013 | 33% | 3% | 23% | -1% | 0.00 |
| 2014 | 16% | 14% | 6% | 10% | 0.01 |
| 2015 | 17% | 4% | 7% | 0% | 0.00 |
| Average Return: | 10% | 4% | Sum: | 0.30 | |
| Covariance: | 0.08 | ||||
The covariance can take on any value and therefore it is hard to interpret the number. We have no idea if this is highly correlated or not.
Correlation tells how strong the relation between X and Y is.
The most important property of the correlation coefficient is that its value is always between -1 and 1.
It is positively correlated if the correlation coefficient is positive and are highly correlated related if the correlation coefficient is closer to 1.
It is negatively correlated if the correlation coefficient is negative and are highly correlated if the correlation coefficient is closer to -1.
Here’s how to compute the correlation coefficient:
| Return | |||||
| Year | X | Y | (Xj – X̄) | (Yj – Ȳ) | Covariance Term |
| 2011 | -50% | -35% | -60% | -39% | 0.23 |
| 2012 | 33% | 33% | 23% | 29% | 0.07 |
| 2013 | 33% | 3% | 23% | -1% | 0.00 |
| 2014 | 16% | 14% | 6% | 10% | 0.01 |
| 2015 | 17% | 4% | 7% | 0% | 0.00 |
| Average Return: | 10% | 4% | Sum: | 0.30 | |
| Standard deviation: | 34% | 25% | Covariance: | 0.05 | |
P X, Y (Coefficient of Correlation) = 0.05/(34% x 25%)
P X, Y (Coefficient of Correlation) = 0.05/0.09
P X, Y (Coefficient of Correlation) = 0.5(9)
This means that X and Y are positively correlated.
Exam Secrets Cheat Sheet
No worries, your information is safe with me. I hate spam too!
My Complete Course students pass the CMA exam at double the global CMA exam pass rate of 35%. This is possible due to the personalized 1-on-1 coaching support they receive throughout their exam prep program.
Below you’ll find an example of a mini-lesson that helped my student, Syed, understand the difference between covariance and correlation.
Syed didn’t have any study materials before finding CMA Exam Academy so he opted for my Complete Course to gain access to the ultimate toolkit for the CMA exam preparation.
Until our next lesson,
Hi, I’m Nathan Liao (aka the CMA Coach)! For the last 10 years, over 82,000 accounting and finance pros came knocking at my door seeking guidance and help. If you’re also aiming to conquer the CMA exam on your very first try—without wasting away time or money—you’ve found your ultimate guide. Dive in deeper to discover more about me and the dedicated team that powers CMA Exam Academy. Click here and let’s embark on this journey together!
